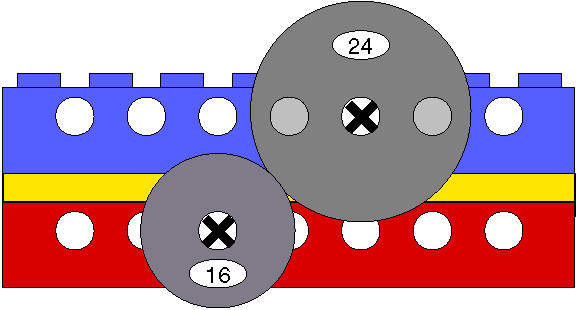
Using Lego to integrate Mathematics and Science in an Outcomes Based Syllabus.
Stephen Norton
QUT
Abstract
Integrated learning has been put forward in curriculum documents as a means
to add meaning and context to mathematics and science learning. However,
few models of practice exist to guide teachers’ in implementing this process.
This paper examines an educational researcher’s and a practicing teacher’s
challenge to use student construction of Lego artefacts as a tool for the
learning of mathematics and science concepts through technology practice. It
was found that the activities afforded opportunities for students to
demonstrate numerous outcomes, that explicit scaffolding was needed by
some students and that some students achieved at outcome levels beyond
those expected of their Year. The findings have implications for the use of
activity in the teaching of mathematics and science where syllabus
documents demand specific outcomes.
Introduction
Papert, (1980) coined "constructionism" and defined it as "Giving children good things to do so that
they can learn by doing much better than before." What Papert had in mind was that children could
learn mathematics effectively by building artefacts and programming simulations. The work of
Vygotsky (1987) and von Glaserfeld, (1987) have further informed the move towards viewing
knowledge as something that individuals construct via interactions with the environment and the
learning paradigm they described was termed "constructivism". Thus, in essence, constructionism is
an extension of constructivism in that like constructivism it emphasises the building of knowledge
structures, but then adds to this that the learner is learning in a context of constructing a public entity
(Papert & Harel, 1991).
The American Association for the Advancement of Science (1993), through Project 2061, actively
promoted the inclusion of technology in the school curriculum and also recommended that technology
could be used as a vehicle for learning science and mathematics. Likewise there has been a shift in
mathematics teaching and learning in the last two decades towards increased emphasis on powerful
ideas associated with mathematical processes (Jones, Langrall, Thorton, & Nisbet, 2002). National
Council of Teachers of Mathematics (NCTM) Standards (2004) has encapsulated this trend world wide
by giving pre-eminence to five process standards: problem solving, reasoning and proof, connections,
communication and representation. This shift in curriculum approach towards communication of
reasoning, contextual problem based learning and integration (both within the subject domain and
across subjects) has found expression in attempts to integrate science and technology with
mathematics. For example, the New Basics curriculum documents (Education Queensland, 2001) has a
strong emphasis on integrated learning. This document encourages teachers to use integrated
community based activities, where the role of the teacher is one of mentoring while students engage in
tasks that are relevant and authentic to the students. Other curriculum documents have recommended
an approach to mathematics teaching and learning that is integrated or transdisciplinary and where the
mathematics is embedded in authentic contexts (e.g., Queensland Studies Authority, 2003). The use of
authentic contexts tends to enable students to develop modelling capacities that need greater
mathematizing and the conceptual use of mathematics (e.g., Nason & Woodruf, 2003).
Part of the reason for the integration of mathematics and science is the perception that falling student
enrolment in "hard sciences" can be attributed to the isolated and fragmented curriculum where
students see these subjects as not relevant (Malcolm, 2002).
McRobbie, Stein, and Ginns (2001) have
suggested that science set in a technological setting is worth examination since technology is part of the
world lived in and experienced by students. Papert and Harel (1991) recommended Lego construction
combined with programming (Lego Robotics) so that students could engage in the building of active
models. In contrast to the view that students ought to construct knowledge, is that students can learn
effectively from direct instruction where the teacher’s primary role is to deliver careful explanations
that take account of cognitive load (e.g., Cooper, 1998; Pollock, Chandler, & Sweller, 2002).
Several studies (e.g., Bergen, 2001; Mauch, 2001, McRobbie, Norton, & Ginns, 2003)
have reported the strong motivational potential and development of problem solving
strategies through working with Lego Robotics. In addition, Levien and Rochefort
(2002) commented on Lego Robotics as a suitable medium to explore engineering
principles with tertiary students. Recent research into Lego Robotics in middle school
years indicates that many opportunities for extracting science and mathematics
principles from technology-based activities are not capitalised on, the science and
mathematics remaining implicit (e.g, McRobbie, Norton & Ginns, 2003). A particular
concern has been teachers’ difficulties in making the links between the technology
activity of Robotics and other syllabus outcomes. McRobbie et al, (2003) also showed
how the programming feature of Lego Robotics had the potential to absorb most of
the students’ problem solving endeavours and thus the science and mathematics
associated with the construction and mechanical operation of the robots became a
secondary concern of both students and teacher.
The mixed results of using Lego Robotics as a medium for the learning of science and
mathematics has prompted this research to investigate the potential of using Lego
construction as a tool to facilitate science and mathematics learning within the context
of technology practice, without programming. Of particular interest was what types
of scaffolding needed in order for students to learn science and mathematics. Thus
this paper focuses on the planning for learning, enacted pedagogies, types of student
outcomes and assessing student learning.
Design and Methods
The method used is participant observation. A rationale for this method is described
by Glesne and Peshkin (1992, p. 39):
Through participant observation, through being part of the social setting – you
will learn first hand how actions of your and others correspond to their words,
see patterns of behaviour, experience the unexpected, as well as the expected,
and develop a quality of trust with others that motives them to tell you what
otherwise they may not.
In this process of participation the researcher and the usual classroom teachers
collaborated in planning, while the researcher taught most of the 2 hours lessons over
a 10 week period as an intervention. Prior to beginning the intervention the researcher
and Jill (main collaborative teacher) matched science outcomes (Queensland School
Curriculum Council, 1999) and mathematics outcomes (Queensland Studies
Authority, 2003) with construction activities related to the "Simple and Powered
Mechanisms" kits (Lego Educational Division, 2003) that were designed to help
students learn engineering concepts. The kits contained a motor, various cogs and
pulleys, various blocks, axles, connecting pieces as well as instruction booklets.
Subjects:
The subjects were 46 Year 7 students in two classes in a State middle school in
Brisbane. The school was a trial school for New Basics Curriculum (Education
Queensland, 2001) that attempts to integrate the teaching of subject domains of
science and mathematics through authentic project based tasks. The classroom
teachers were also part of the study. Jill and Tony (all names are pseudonyms) were
experienced primary school teachers who had a passion for science. Unfortunately,
Tony replaced the original classroom teacher of the second class half way through the
study, thus Jill was more involved in the planning and evaluation and the balance of
evidence reported reflects this situation.
Data collection
The collection of data included a reflective journal written by the researcher and on
going tape-recorded interviews with the teacher and student construction and
presentations as well and digital photographs of artefacts. In addition, the students’
interactions with objects, peers and teachers, student planning and construction of
artefacts, and their explanations of how things worked were recorded on video tape.
Students’ artefacts including their planning sheets, written explanations and their
explanations on written tests were also collected. In the second week of the study the
students were given the task of planning and constructing an artefact that either served
a practical need or modelled a useful product. At the end of the study students
repeated the planning and construction activity. Students’ plans and artefacts were
compared. The students were also given pre-intervention and post-intervention pencil
and paper tests on science and mathematics concepts. Throughout the study the
teachers acted as observers and documented student activity that indicated an outcome
had been met.
Analysis:
A hermeneutic cycle (Guba, & Lincoln, 1994) was employed in developing and
testing assertions as the study progressed. Emerging assertions were discussed with
the teacher and colleagues and tested and refined in the light of further evidence. The
video and audio records of activity and interviews were listened to and key elements
transcribed and categorised according to emerging assertions. Triangulation involved
the use of multiple data sources identified above and this maximised the probability
that emergent assertions were consistent with a variety of data.
In seeking an analytic frame to help the assessment criteria the author used the Payne
and Rathmell (1977) triangle that shows two way interactions between representations
(concrete and pictorial), language and symbolism. To guide the assessment process
the author devised a series of indicators associated with each outcome. For example,
in relation to the mathematics outcome associated with ratio Level 5 "Students
identify and solve multiplication and division problems involving positive rational
numbers, rates, ratios and direct proportions using a range of strategies" (QSA, 2003,
p. 21 the following indicators for ratio were developed:
Level 4: Students construct gearing but can not articulate the relationship that
exists in terms of magnitude (e.g., "The motor is connected to the gears which
makes the wheels turn"). This statement does not attempt to describe the
relationships that exist between the gear sizes nor how this effects their
functioning. In essence the student’s understanding is confined to the concrete
level and this is reflected in the language used. The statement does not give
explicit recognition to the concept of ratio.
Level 5: Qualitative explanations: Students construct appropriate gearing and
can explain it in qualitative terms (e.g., "The small driver goes around lots of
times and this makes the bigger follower go around a few times, this is good
for power"). In this instance the student was able to articulate the nature of the
relationship in terms of direction and magnitude but only in a qualitative way.
There was evidence of stronger understanding of the concrete representation
and the connections between concrete representation and language reflect this.
Level 5: Quantitative explanations: Student has used the gearing and can
explain it in a quantitative way (e.g., "The drive has 8 teeth, it needs to go
around 5 times to make the follower with 40 teeth go around once. This is
good for a tractor to pull loads"). In this example, the connections between
the material model, language and symbolism are all present and the nature of
the relationship is accurately described quantitatively. This would indicate
relational thinking (Skemp, 1978).
Level 6: Students have used gearing in a novel problem solving context that
illustrates understanding and can explain it in a quantitative way. Students
who use a series of gears to amplify the effect of gearing is one such example
and can quantity this relationship would be and example of this. Thus,
construction and explanation illustrate the students can correctly connect the
representations, language and symbolism associated with ratio concepts.
The mathematics Level 6 indicator above was developed for the outcome statement
Students identify and solve multiplication and division problems involving rational
numbers, rates, ratios and direct and inverse proportions using a range of
computational methods and strategies," (QSA, 2003, p. 22). Similar frameworks
needed to be developed to assess science based thinking.
Results and Analysis
The results are presented as a series of assertions followed by supporting evidence.
Assertion 1: Construction activities give the potential for students to achieve many learning outcomes
in science, mathematics and technology.
In the process of identifying those outcomes that might be developed through the construction activities
the researcher constructed from the Lego plans various levers, pullies, draw bridges, conveyor belts,
drummers, model windscreen wipers, cars, conveyors, merry-go-rounds, turnstile, crane and worm gear
winch. What became apparent was the great amount of mathematics and science understanding
underpinning the construction and explanation of the operation of these artefacts. This work lead to the
identification of syllabus outcomes associated with the Lego activities. In the current Queensland
Syllabuses outcomes are expressed at levels from one to six. One being entry to school level, level 3
outcomes ought to be demonstrated by the end of Year 5, level 4 outcomes at the end of Year 7 and
level 6 outcomes at the end of Year 10. Some focus outcomes are presented in table 1 below. There
were numerous outcomes associates with the activities in the Science Syllabus (Queensland Schools
Curriculum Council, 1999) within the strands of science and society, energy and change over a range
of levels from level 2 to 6. Similarly, in the Mathematics Years 1 to 10 Syllabus (QSA, 2003)
activities were matched to outcomes in the strands of number, patterns and algebra, measurement,
chance and data and space, again across a range of levels. The technology embedded in the activities
was mostly in the strands of technology practice, materials and systems within the Technology Years 1
to 10 Syllabus (QSA, 2003).
Table 1
Sample of syllabus outcomes related to construction activities
Mathematics | Students identify and solve multiplication and division problems involving whole numbers, decimal fractions, percentages, rates, selecting from a range of computational methods, strategies and known number facts (Number 4.3). Students analyse experimental data and compare numerical results with predicted results to inform judgements about the likelihood of particular outcomes (Chance and data 4.1). |
Science | Students collect and present information about the transfer and transformation of energy (including potential and kinetic energy, Energy and Change 4.2) |
Technology | Students generate design ideas through consultation and communicate these in detailed design proposal (Technology Practice 4.2) |
Clearly, the proposed activities provided a rich opportunity for students to demonstrate achievement of
a number of core learning outcomes identified in the three syllabus documents. The problem for the
researcher and Jill was in deciding how to plan, carry out lessons and assess learning such that
outcomes might be documented. Faced with the almost overwhelming planning task of integrating the
outcomes Jill commented:
I guess I am lucky that I am a fairly experienced teacher and I know a fair bit of
science, other wise you would not know what science was in the construction. I do
not think that everyone has that love of science and maths and it is extremely
important (in order to integrate the two).
That is, Jill considered many teachers would not find it easy to link syllabus outcomes with the
construction activities. She commented on the researcher’s teaching plans with respect to the focus on
particular outcomes.
When I do my planning I specifically think of what major point I want to get across
to my kids? What do I want every child to understand? I have to decide what is
pertinent to Year 7 and at what level do I need them to understand. Then before the
actual lesson can begin you have to recap the information that is needed. This can be
a real problem because not everyone in Year 7 is up the "correct" level. I have to test
them first to see where the gaps are and then I have to teach at a Year 7 level but
scaffold the less able students more. I have to help them with the underpinning
knowledge that is missing.
Both the mathematics and science syllabuses (Queensland Schools Curriculum Council, 1999;
Queensland Studies Authority, 2003) are spiral curriculum documents that assume prerequisite
outcomes have been attained. In fact, it may well be argued that they reflect the notion that
mathematics and science are structured and hierarchical bodies of knowledge. Thus, in the sequencing
of outcomes reflect an image of knowledge consistent with Ernest’s (1991) view of mathematical
knowledge as a set of truths and body of structured knowledge consistent with absolutist images of the
nature of mathematics and usually associated with instructivist (Cooper, 1998; Marsh, 2004) teaching
practices. Essentially the same view was described by Galbraith (1993) as the "conventional
paradigm." This view is in contrast to fallibist images of mathematics and science usually associated
with constructivists pedagogies. For Jill this created a tension. She acknowledged that the way current
syllabus documents were enacted was not motivating many students, but at the same time the structure
of the syllabus needed to be reflected in teaching.
They hated it because they felt that they were no good at it (mathematics), and it was
boring. But, on the other hand, many kids in this group need the structure.
Somewhere along the line they have missed out on the structural approaches to all
the concepts including fractions for example.
This statement reflects her view that many students had experienced predominantly instructivist
pedagogy that fostered a negative image of mathematics and science and affected their ability,
however, at the same time she acknowledged that students had missed explicit structuring that they
needed in order to understand difficult concepts. In attempting to account for the need to provide a
focus for student learning so that essential scaffolding was afforded to students, the researcher and Jill
decided to focus on the concept of ratio that had been identified as challenging (e.g, Lamon, 1995),
and science concepts associated with energy and change. Consequently, the lesson planning and
implementation refected this focus.
Assertion 2: Scaffolding in the form of explicit details was needed for some students to make links
between activities and outcomes.
In the early lessons the researcher adopted a relatively unstructured construtionism approach to teaching,
in that the students were asked to construct various artefacts (e.g., "make me a car that can go fast") and
he attempted to hold class discussions towards the end of the lessons to make explicit the underlying
mathematical and science concepts. This approach was an attempt to have the students demonstrates
level 4 of technology practice and level 5 mathematics explanation of ratio. Lesson observations
indicated that to a considerable degree this approach lead to less able students becoming frustrated and
the class discussions were dominated by the few students who had the prior knowledge to link the
activity of construction explicitly to the science and mathematics. In behavioural terms this was
manifested by a few students engaging in off task behaviour and others expressed bewilderment and
disenchantment as one less able student commented; "I just do not know what is going on." For other
students the activities offered an opportunity for cognitive conflict and rich learning. For example when
exploring levers one student commented:
It does not make sense, I am all muddled up". A see-saw is constructed with a
pivot, load and effort. The pivot is in the middle of the lever, but if it was closer, the
other child would go boong. If it was even, then nothing would happen. If the pivot
was close to a light child it would make an easier effort.
Such a statement illustrates an accounting of proportional thinking and the relationships between
leverage, mass and forces. Jill’s comment on the problem of students having different level of
engagement was:
The good kids understand it, but it (ratio) is a concept that needs to be teased out,
you have to bring it down to simplest terms, you have to have a diagram.
In essence what Jill was recommending was alternative representations (a diagram) to
accompany the concrete material and explicit scaffolding to focus students’ attention to the
links between the material models and the underlying science and mathematics concepts.
The researcher’s diary acknowledged the tension between construction and attempting to
teach to specific outcomes:
It is very difficult to use the Lego to set up the science learning, because you are
always struggling with the conflict of them wanting to build and you wanting to
formalise.
Over the course of the study Jill and the researcher consulted after each lesson and as a result of their
reflections and negotiations the pedagogy enacted by the researcher evolved. For example three weeks
into the project Jill commented:
You need to build in more structure, give them structure, but let them explore as well"The
higher end kids, they can do a lot of investigative work, but some in this group have missed out
so you need to simplify it. I did that with fractions, you know, I brought something in and we
would cut it up, a pie or a cake, whatever.
Following this advice, the author attempted to provide more structure in the lessons. The first 15 to 20
minutes of each lesson was spent clearly defining the purposes of the construction task. For example, if
the task was to explore the nature of ratio by having students design build and explain the gearing of a
tractor this task was made explicit and the students were provided with planning sheets to facilitate
their thinking about ratio. In addition, it was considered that the concept of ratio (pre-requisite
knowledge) ought to be revised in contexts that ought to have been familiar to them such as identifying
the ratio relationship present when there were 2 while balls and 6 green ones. The students were also
asked to reflect on ratios that they were likely to be familiar with in the course of their daily life such as
bicycle gears. Unfortunately, this was a "post activity" thought and the revision of ratio did not occur in
this study.
The author attempted to hold debriefing discussions at the conclusion of each class and this was used as
an opportunity to link the formality of science and mathematics outcomes with the construction
activities. Jill noted that student involvement in classroom discussion was "patchy, that is some
students consistently contributed to class discussion while other appeared disengaged." The author and
Jill agreed that in future investigations each group would be asked to give a class presentation
explaining their artefact and would be graded according to the scientific and mathematical thinking
they demonstrated.
Jill expressed her approval for a mix of board work with standard revision of concepts and practice on
ratio questions and construction of artefacts. While students worked in pairs or in groups of three to
design, make and explain, the author walked between groups and much of his scaffolding was directed
towards eliciting student explanations of their artefacts.
The practice of the formal setting out of mathematical problems was to happen in homework time or in
subsequent non construction lessons. Jill stated that although she believed this ought to happen, over
the life of the study it occurred to a very limited degree, simply because Jill had other curriculum
material to be covered in mathematics and science. This failure to utilise the homework time to support
the learning that occurred during the construction activities was noted by Jill and the author as a factor
that limited the potential to make connections between the activity occurring during the construction
and planning phases and specific outcomes in mathematics and science.
In conclusion, in catering for the needs of different students, teachers needs to be aware of students’
perquisite knowledge and provide the level of scaffolding that different students need in-order to
engage in concept related discussion and to forge the links between the various representations. Such
scaffolding includes clearly setting tasks requirements, class discussions based on student
presentations, a mix of board work and book work, the use of homework to revise concepts and
questioning of students about how their constructions operated. While such an observation has been
noted previously, in the case of technology mediated activities, appropriate scaffolding may take on
additional significance. Put simply there are more opportunities for students to be cognitively
disengaged and more ways to fail to make appropriate links between representations. On the other
hand, it could be argued that when learning within a technology practice setting there are more ways to
be cognitively engaged and more opportunities to make links between representations and thus develop
powerful understandings.
Assertion 3: Year 7 students are expected to achieve outcomes at level 4, but a number achieved at
levels beyond this.
There were two main ways the author attempted to assess and document student
learning. The first was via pencil and paper pre and post-tests on the mathematics and
science concepts under study. Some questions were simply definitions while other
questions required quantitative expressions of proportional reasoning to gain full
marks, for example:
Examine the diagram of pulleys (diagram included in script). If the circumference of pulley A
is 20 cm, the circumference of pulley B is 40 cm and the circumference of pulley C is 10 cm
and pulley B I spun twice, describe how pulleys A and C will spin. Explain why this will
occur.
The correct answer to such question would be an indication that the student understood ratio at level 5
(Quantitative). Other questions were more open, for example, students were given the number of teeth
on various gear cogs and asked to use their knowledge of bicycles to create a matching pair that would
help the bike go fast, and to give a possible explanation that would be correct and complete (level 6).
Scoring was on the basis of correctness and completeness of explanations, and each item was allocated
2 marks. Answers that had correct quantitative responses as well as their explanations were allocated
full marks. The results for the pre-test and post-tests for science and mathematics are presented in
Figures 1 and 2.

Figure 1: Pre-Post Test Results in Science
f
The box plot gives a visual expression of the pre-test and post-test results for science, the pre-test
results being on the left and the post-test on the right. The box plots indicate that the median and in
particular top 75% of scores improved considerably. A number of students performed poorly in both
pre and post-tests. The paired samples correlation coefficient between pre-test and post-test results was
low, (r(42)=.30, p=.047) indicating that a high score on the pre-test was not a good predictor of
performance on the post-test for science.
Box plots of the mathematics pre-test and post-tests indicated that the scores were
generally higher in the post-test. The pre and post test results indicated that the pretest
score in mathematics was a reasonable predictor of the post-test score, (for
example r(34)=.64, p<.000).

Figure 2: Pre-Post Test Results in Mathematics
As with science there were some students who improved in their rest results and some who made
minimal improvements on the test.
In the initial construction phase almost all student constructions did not take account of mathematics
principles such as ratio and science associated principles including friction and leverage (the exceptions
being those four groups of boys who had extensive Lego kits at home) and for all groups the
explanations were not connected to science or mathematics principles. For example, a pair of girls
constructed the following helicopter in week 4.

Figure 3: Week 4 Helicopter
This helicopter has a simple direct drive to one set of blades. Their explanation of the
mechanics was as follows:
The motor makes the propellers go round and they make the helicopter work. The propeller on
the top gives off a large amount of wind and the helicopter nearly flies. The tail is for balance
and it has another propeller attached to it. When the ‘copter’ vibrates this propeller nearly turns
around, we are still re working it.
This description conforms to Level 3 of the Energy and Change strand of the syllabus
"Students understand the effects of forces on the shape, motion and energy of
objects." (Queensland School Curriculum Council, 1999, p. 79) but does not contain
evidence of mathematical outcomes. The figure below is a later construct.

Figure 4: Week 8 aeroplane
The girls’ second artefact used a series of gears to drive both the propeller blades and
bevel gears to the back wheels of the plane "for taxiing up the runway." While able to
construct in a more sophisticated way their explanations on the working remained one
of describing the cause and effect and they did not try to quantify their explanation
not even to qualify the relationship in terms of more or less turns needed to drive a
following gear. In this regard, the explanation remains at level 3 and certainly the did
not show evidence of attaining level 5 of the number strand "students identify and
solve multiplications and division problems involving positive rational numbers,
rates, ratio and direct proportion" (QSA, 2003, p. 21). That is, it did not attempt to
describe the artefact in terms of rates or ratio and there was no evidence in the
students’ explanations that this concept had been developed over the life of the study.
The motor turns the shaft that turns the propeller, and the middle gear turns the
second propeller, which turns the axle which turns the wheels. The back gear is a
bevel gear. It is pretty slow. If the propellers could go fast it might fly, but it can’t.
The students’ explanation does not account for the science principles that are involved (force, friction,
& energy transformations) and the science outcome remains at Level 3. Thus, while the construct was
mechanically more sophisticated than the helicopter, their explanations of the artefact had not met a
higher outcome indicator.
Other students did account for science principles in their final artefacts. Three boys made a game of
shooting a target.

Figure 5: Target shooter.
Their written explanation was as follows:
The target practice machine can be motorised or you can make it launch manually,
the missile is made of two small boxes and some teeth that grip onto the gear
connected to the motor. The flat surface allows a missile to slide and if it was
enough velocity it will shoot off and hit the target. The wall at the back stops the
missile as far back as it goes, where the missile stops it’s the fastest it can go.
This statement indicates a level of understanding at the level 4 of the science syllabus "Students
understand that there are different forces which affect the motion, behaviour and energy of objects."
(Queensland School Curriculum Council, 1999, p. 79). Their original explanations of the non
motorised quad chair was rich in a description on how it was made but not how it functioned, thus in
terms of science outcomes their explanation was level 3. The boys did not attempt to describe the
shooter in mathematical terms, they did not discuss the relationship between the diameter of the driver
cog and missile velocity or describe the trajectory in quantitative terms, such reasoning would have
equated to a level 5 outcome (QSA, 2003, p. 25);
Students identify when relationships exist between two sets of data and use functions expressed
in words or symbols, or represented in tables and graphs to describe these relationships that are
linear and express these using equations.
Some students improved markedly in their ability to explain their products in
mathematical terms. In week 2, two female students who had been identified by the
teacher as mathematically very capable had designed a car for all terrain travel. It
featured (Figure 6) the use of a simple pulley system to drive a four wheel drive
"tractor" using a 40 tooth cog gear for rear wheels to "help with grip."

Figure 6: All terrain car, week 2.
The design illustrates that the students did not understand the relationship between
wheel diameter and circumference. When they tested the car, it would run on a desk
where slippage negated the lack of synchronisation between the front and back
wheels, but would not run on carpet where the front wheels acted as a brake on the
back wheels. In this instance the students did not recognise the significance of the
relationship between the different diameters and the distance each wheel would
travel. The misconceptions the students manifested in terms of circumference, rates,
ratio and direct proportion indicate that the students were operating at with error at
level 3 of the number strand. The critical issue here is they could not apply their
number skills to in this situation. (They had just recently demonstrated computational
competency in the attributes of circles, ratio relationship between diameter and
circumference, in their normal mathematics class. In this regard their mathematical
knowledge might be described as "instrumental" (Skemp, 1978). In contrast their
construction of a tractor in week 8 demonstrated a much better use of the concepts of
ratio (Figure 7).

Figure 7: Low geared tractor, week 8.
The students’ description of a tractor several weeks later was an excellent display of
mastery of ratio.
The 8 teeth gear on the motor (driver) will turn the 40 teeth gear underneath it, (the
driver) will turn 5 times, then 8 gear on the same bar as the 40 teeth gear will also
turn 5 times, when the 8 gear turns 5 times, the gear with 40 teeth will turn once,
making the 24 teeth gear that is behind the wheel turn around about 1 and ¾ times.
The students were aware that the driver gear had to turn 25 times to effect an outcome of "about 1 and
¾ times," this is remarkably accurate. This explanation is consistent with Level 6 of Number strand
(QSA, 2003, p. 22):
Students identify and solve multiplication and division problems involving rational
numbers, rates, ratios and direct and inverse proportions using a range of
computation methods and strategies.
The students’ abilities to apply the knowledge to unfamiliar contexts indicates an understanding of
ratio as described by Skemp (1978) as relational. The author does not imply that the students could not
do multiplication and division previously, but there is strong evidence in the final product that their
thinking about ratio had progressed and that they could apply this knowledge to authentic situations.
In summary, the degree to which students made progress on pencil and paper tests varied considerably,
as did their demonstration of outcome indicators and they had attained better outcomes in science and
mathematics. Some students demonstrated thinking which indicated that they were achieving at levels
well in advance of what was expected in Year 7.
Assertion 4: Student manifestation of science and mathematics outcomes were
directly related to the technology activities.
Jill commented favourably on the activities as a means of teaching science and
mathematics, for example she stated:
I do believe that they have a far better idea of ratio. I think that the activities really cemented
ratio. The practical application with the gearing that was really good, because they had a
visual as well a practical application and it helped them to put it all together. It was a great
grounding and is going to stand by them for year eight and beyond, they will always recall
this.
Further, Jill noted lack of student motivation in the traditional way mathematics was
taught to this class:
They were very de-motivated in terms of maths. They hated it, because they felt that they
were not good at it. That is why I have adopted a thematic approach.
Jill commented on student motivation over the course of the study:
By and large, with the exception of probably about four people in the class, I believe that each
child valued it. Clearly, to me learning took place. They loved playing with it, you know, the
actual building of it. I think there was a sense of commitment there, the commitment to keep
working for so many weeks.
Clearly, Jill considered that student motivation during the construction activities was a
factor that contributed to their mathematics learning. However, she recommended that
increasing the connections between the activities and outside experiences of the
children such as "thrill rides and roller coasters and computer programs about how
thing work." The importance of linking various representations of the ratio concept
has been noted in research literature (e.g., Ben-Chaim, Fey, Fitzgerald, Benedetto, &
Miller, (1998); Lamon, 1995). Jill further recommended that links between
construction activities and formal mathematics be made.
I would keep them in the same sort of structure because this group needs structure, structure
but let the kids explore and talk as well. You need to make links to board work, to set time
limits, have set class discussion. They need a bit more time to absorb the information and
build the artefacts because some are thinking, "am I doing this right?"
The second teacher, Cameron supported the Jill’s evaluation of students learning and
like Jill he recommended that the links between the activities and formal mathematics
be made more explicit:
It is definitely more hands on (than a normal mathematics lesson) and appeals to a student
who likes to see things in their hands and count gears and so on. But, maybe some students
didn’t see the structure (underlying mathematics concept)"For that to happen maybe some
needed more direction, a bit more board work. Do the ratio with board work and then tell
them, "OK lets apply that knowledge to building with this Lego now."
In summary, both teachers believed that the gains in student achievement of specific mathematics and
science outcomes were mostly related to student engagement with the Lego technologies. Both
teachers also recommend more structure and scaffolding so that students could more readily make the
links between construction and other representations including formal mathematics and science
language and symbols.
Discussion and Conclusions
In the introduction, a rationale for using problem solving and reasoning associated
with personal context was given (e.g., Education Queensland, 2001; Jones et al.,
2002; NCTM, 2004). A number of authors (e.g., McRobbie, Norton & Ginns, 2003)
expressed a concern that the powerful ideas associated with construction activities,
including Lego construction and robotics could remain latent. With this in mind the
author made every effort to make the links between syllabus outcomes and activities
in the planning of lessons. The data presented in assertion 1 indicated that the Lego
construction activities are rich in opportunities to achieve outcomes listed in the
Queensland Mathematics, Science and Technology Syllabuses. In the case of
technology most of the outcomes were associated with the technology practice of
planning, constructing and evaluating artefacts. The study indicated that explicit
links between specific syllabus outcomes and construction activities could be made;
however, making such links was not a trivial task. A major problem for the author
was to recognise the mathematics and science embedded in the activities and to link
these to specific outcomes. The finding that there were so many potential outcomes,
that the author ultimately had to choose a few to make explicit. Thus, in this study
much of the underpinning science was never made explicit in class discussions. This
was reflected in the relatively limited use of science explanations that many students
gave in relation to the functioning of their artefacts, while other students made their
own connections between their constructs and the science that they knew.
Related to the challenge of identifying outcomes was that of assessing the levels of
outcomes, the challenges in identifying student thinking in mathematics been noted
previously (e.g., Gailbraith, 1993). It is a problem when operation within the
educational paradigm of conventional paradigm of scientific enquiry and the
intructivism teaching approaches associated with it. This study indicates that
evaluating student thinking in constructivism paradigms is a difficult task and not
made easier by an outcomes approach to reporting. The task of collecting and
evaluation students thinking associated with their construction and explanations of
their constructs was an ongoing interpretive process that involved the teachers
collecting and recording multiple sources of data. The framework based on the degree
of connections that students made between the different representations of the
mathematics and science concepts presented in the analysis section of Design and
Methods was a useful means to match student explanations and constructs to specific
syllabus outcomes. However, refinement of this tool for use on different outcomes is
needed. The difficulties were compounded by the group nature of the construction
tasks, in particular how was a mark for the group to be allocated to the individuals
within the group?
The results summarised in assertion 2 illustrate that the author and Jill were aware that
there was a danger of key concepts remaining implicit and Jill encouraged the author
to move his pedagogy away from some sort of lassie faire constructionism and
towards "directed constructionism." This was evidenced in her repeated
recommendation for more structure in the lessons. While the pedagogy that Jill was
recommending and the author was attempting to implement was not "traditional
teaching," it had many of the elements of instructivism (Marsh, 2004) including
careful verbal instruction at the beginning of the lesson, orientation of students in
relation to key concepts and expected outcomes and there were to be opportunities to
reinforce via practice. Jill’s concern was most apparent in relation to those students
who struggled to make the links between the construction tasks and the abstraction of
mathematical ideas. The idea that teachers believed that students who struggle need
more direct instruction pedagogy has been noted previously, (e.g., Norton, McRobbie
& Cooper, 2002). To take account of the differing needs of students of different
abilities and with different prerequisite knowledge the author allocated increasing
time to the processes of abstracting mathematics and science principles. While, the
major part of each lesson was still in the context of students working in groups to
design, make and explain their products, teacher intervention increased over the life of
the study. In order to encourage students to make the links between various
representations (e.g., the machines, plans and the formal language of mathematics and
science) the author and Jill agreed to further emphasise student explanations. It was
recommended that each group would present their product and be rated on the quality
of their explanations on how it worked. In this way the author was attempting to add
focus and structure to student discourse. In short, the activities provided ample
opportunity and stimulus for student discussion, the challenge for the teaching team
was how to scaffold the lesson such that the discussion was purposeful.
The results of this study presented in assertion 3 indicate that the use of concrete
materials in the context of design, construction and evaluation activity provides rich
opportunity to connect mathematics and science concepts and to promote the learning
of powerful ideas such as ratio, force and energy transfer. The student results on
pencil and paper tests, the student constructions and explanations indicated that some
students made considerable progress on specific science and mathematics outcomes.
On the other hand other students did not demonstrate improved outcomes. The
teachers’ comments suggested that the learning gains were mostly due to student
involvement in the intervention, rather than some other factor such as maturation or
alternative learning activities. Given the difficulty level of these concepts such has
ratio, (Karplus, Pulos, & Stage, 1998; Resnick & Singer, 1993) and rate (velocity)
such improvement in results supports the suggestions of those authors who
recommend multi representations of mathematics and science concepts, including the
use of manipulative material (e.g., Ben-Chaim, et al. 2002; Lamon, 1995). The results
encourage the adoption of an integrated approach to teaching powerful ideas, as
reflected in reform curriculum documents (e.g., Education Queensland, 2001) and
situated learning contexts (Brown, Collins, & Duguid, 1989). More specifically, the
results support the suggestion that Lego is a very useful manipulative for the learning
of mathematics and science.
The study illustrates that there were challenges in attempting to meet varying student
needs for scaffolding, and these were manifested in difficulties in planning and lesson
conduct. There were also substantial challenges in assessing student progress and to a
degree these remain unresolved. However, the study adds to our capital of
pedagogical knowledge about how the use of tools such as Lego can be used to foster
the kinds of social relationships and engagements with authentic and contextual
problems learning. As noted by Papert (1980) "giving children good things to do" "
can foster powerful learning, but the task of achieving connected learning is by no
means simple. The study also indicates that significant professional development may
be needed to help teachers to plan, conduct and evaluate lessons.